生存分析#
1. 生存概率#
在分析存活时间时,会出现不同于目前为止的讨论的问题。一个问题是如何处理受试者退出研究的问题。设我们测试一种新的癌症药物。当一些受试者死亡时,其他受试者可能认为新药无效,并决定研究结束前退出研究。这类研究使用的术语是生存分析(survival analysis)。
这种方法也用于分析其他领域的类似问题。例如:可用于研究机器在坏掉之前的寿命有多长;或人们订阅邮件列表的时间(其中”死亡”对应的是取消订阅邮件列表)。
1.1. 删失#
进行生存分析的难点在于,在一项研究结束时,许多个体可能还”活着”。在统计学中,对于只能部分知道的测量值的表达方式是删失(censoring)。若未知数据位于生存阈值右侧,则称为右删失,反之称为左删失。
举个例子,考虑一个邮件列表,其订阅者分为两个子组。第一组很快就厌倦了邮件,三个月后就会退订。第二组人很喜欢,一般会订阅一年半的时间。
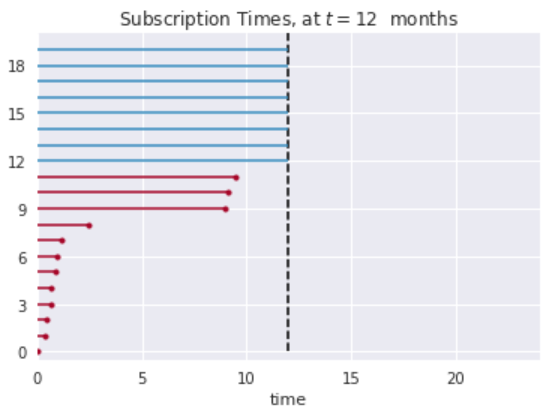
红线表示有退订行为的个人的订阅时间,蓝线表示没有退订行为(被右删失)的个人的订阅时间。若要求估计总体的平均订阅时间,而又本能地决定不包括被右删失的个人,很明显会严重低估真实的平均订阅时间。
1.2. Kaplan–Meier 曲线#
若一些受试者在研究中期增加了他们的隐私设置,即在研究结束前禁止我们对他们进行监控,就会出现类似的、进一步的问题。而处理这些问题的一个巧妙方法是用 Kaplan -Meier 曲线来描述这类数据。首先,时间被细分为几个小的时期。然后计算受试者在给定时期内存活的可能性。生存概率由以下公式给出
其中,\(p_k\)为第\(k\)期存活的概率;\(r_k\)为第\(k\)天之前仍有风险(仍被跟踪)的受试者人数,\(f_k\)为第\(k\)天观察到的失败人数。
下面的数据给出了苍蝇的基因型和存活的天数。由于工作对象是苍蝇,故不需要担心左删失的问题:因为知道所有苍蝇的出生日期。不过确实有误杀一些或若一些逃跑的问题。因为实际上并没有观察到它们因自然原因而死亡,这些将被右删失。
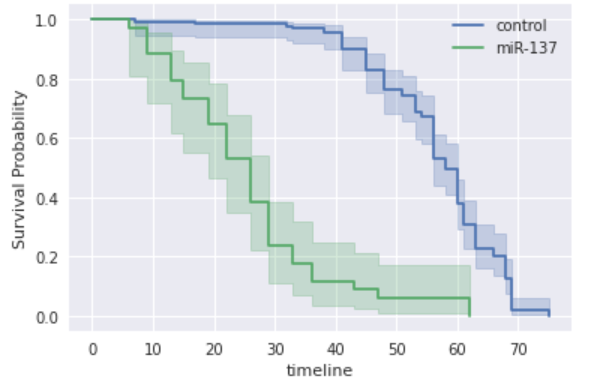
2. Weibull 分布#
Weibull 分布可靠性数据或寿命数据建模的最常用分布。由于它最早是由 Fréchet 确定的(1927 年),但由 Weibull 详细描述的(1951 年),故有时它也以 Fréchet 分布为名。
Weibull 分布有两个参数,可处理增加,减少或恒定的故障率。
其中,\(k > 0\)为形状参数,\(λ> 0\)为标度参数(可省略),其互补累积分布函数是拉伸指数函数。
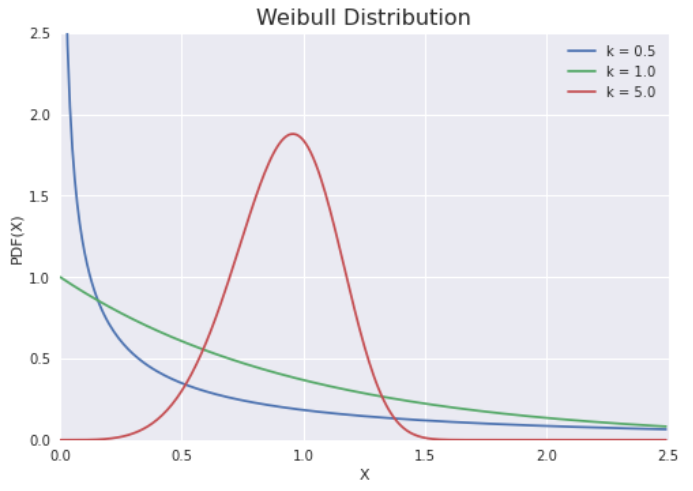
若数量\(x\)是”失效时间”,则 Weibull 分布给出失效率与时间功率成比例的分布。
\(k< 1\)表示故障率随时间降低。若存在显著的”婴儿死亡率”,或有缺陷的物品早期失效,且随着时间的推移失败率随着缺陷物品被淘汰出局而发生,则会发生这种情况。
\(k = 1\)表示故障率随时间不变。这可能表明随机外部事件导致死亡或失败。
\(k>1\)表示故障率随时间增加。若存在”老化”过程,或随着时间的推移更可能发生故障的部件,则会发生这种情况。一个例子是具有内置弱点的产品在保修期满后很快就会失败。
