概率与分布#
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import patches
from scipy import stats
plt.style.use("fast")
1. 条件概率#
1.1. 定义#
古典概率
无需实验
没有误差
可能性有限且大小相等
条件概率
指事件\(𝑨\)在事件\(B\)已发生条件下的发生概率
表示为:\(P(A|B)\),\(P(AB) = P(B|A)P(A)\)
1.2. 事件的运算#
在概率论中,考虑一个样本空间 Ω,它是所有可能结果\(ω\)的集合,以及它的子集的集合\(F\),其结构为 σ 代数,其元素称为事件(event)。
有限可加性
加法定律
独立性
推论 1
1.3. 全概率公式#
完备事件群:任意两事件互斥,所有事件的并集是整个样本空间(必然事件)
全概率公式:对完备事件组\(B_{i}\),若事件都有正概率,则对任一事件\(𝑨\)都有如下公式成立
2. 随机分布#
2.1. 随机变量#
随机变量
一个真实的随机变量 X 是一个(可度量的)从\(Ω\)到\(ℝ\)的映射。
离散随机变量
若一个随机变量\(X\)在\(ℝ\)的一个子集中取值,其取值个数可度量,则说它是离散的。
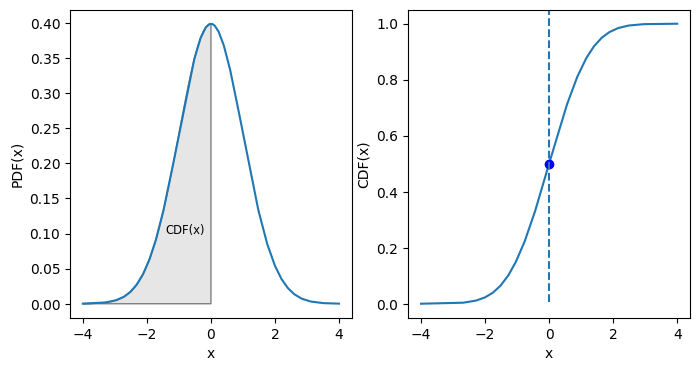
2.2. 分布函数#
概率质量函数(Probability Mass Function,PMF):离散随机变量在各特定取值上的概率。
概率密度函数(Probability Density Function,PDF):连续随机变量的 PMF。
累积分布函数(Cumulative Distribution Function,CDF):PDF 的积分,是分位数的倒数。
\(k\) 个随机值的和 \(S_{k} ≥ 4\sqrt{k}\)
生存函数(Survival Function,SF):1 - CDF,给出大于给定值的值的概率。也可解释为数据”存活”超过某个值的比例。
百分点函数(Percentile Point Function,PPF):CDF 的逆函数。
逆生存函数(Inverse Survival Function,ISF)
3. 常见离散分布#
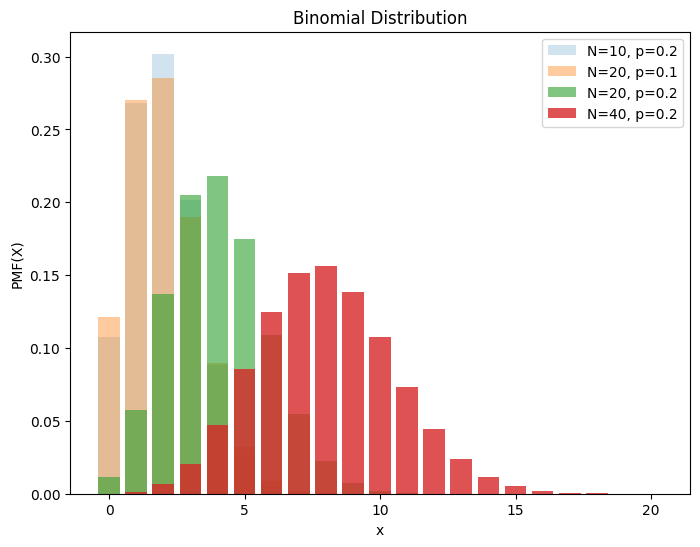
3.1. 二项分布#
设试验 E 只有 2 种可能结果 A 和 Ā,则称 E 为 Bernoulli 试验,将此试验独立重复\(n\)次,即为\(n\)重 Bernoulli 试验(如放回抽样),其结果的发生概率服从 Bernoulli 分布,也叫 0-1 分布。
将后者的试验结果\(X\)扩展为 ℤ,则其中一个结果\(k (k ∈ ℤ)\)的发生概率\(P\{X = k\}\)服从二项分布
其名称源于,其 PMF 形式类似二项式定理
假如投一个正六面体的筛子 256 次,则得到 32 次 6 的概率,可由如下方式计算
def binomial_test(n, p, checkVal):
p_oneTail = stats.binomtest(checkVal, n, p, alternative="greater")
p_twoTail = stats.binomtest(checkVal, n, p)
return (p_oneTail.pvalue, p_twoTail.pvalue)
n, p = 256, 1 / 6
checkVal = 64
p1, p2 = binomial_test(n, p, checkVal)
print(
f'The chance that you roll {checkVal} or more "6" is {p1:5.3f}, and the chance of an event as extreme as {checkVal} or more rolls is {p2:5.3f}'
)
The chance that you roll 64 or more "6" is 0.000, and the chance of an event as extreme as 64 or more rolls is 0.001
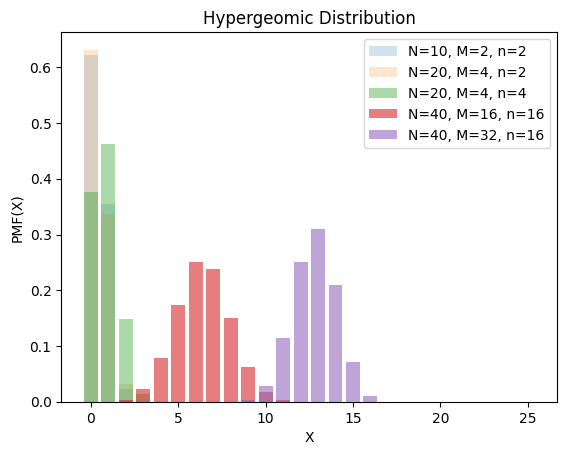
3.2. 超几何分布#
一批产品共\(N\)个,其中废品\(M(⩽ N)\)个。随机抽取\(n\)个,含\(m\)个废品的概率服从超几何分布,相当于不放回抽样的二项分布
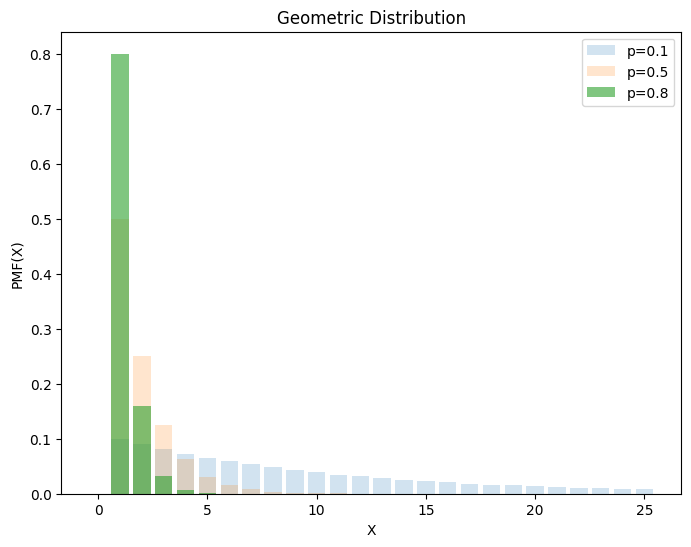
3.3. 几何分布#
在\(n\)次 Bernoulli 试验中,第\(k+1\)次才第一次成功的机率服从几何分布,记作\(X ∼ G(p)\),也可以理解成连续失败\(k\)次的概率分布。
几何分布得名于几何级数:
3.4. 负二项分布#
已知合格率为\(p\)时,进行\(n\)次实验,抽到合格品\(r\)个,服从分布负二项分布,即重复\(n\)次的几何分布
此分布得名于负二项展开式
ns = [10, 20, 20, 40]
ps = [0.8, 0.4, 0.8, 0.8]
alphas = np.arange(1, len(ns) + 1) * 0.2
X = np.arange(0, 26, 1)
_, ax = plt.subplots(figsize=(8, 6))
for n, p, alpha in zip(ns, ps, alphas):
y = stats.nbinom(n=n, p=p).pmf(X)
ax.bar(X, y, label=f"n={n}, p={p}", alpha=alpha)
ax.set(xlabel="X", ylabel="PMF(X)", title="Negative Binomial Distribution")
ax.legend()
plt.show()
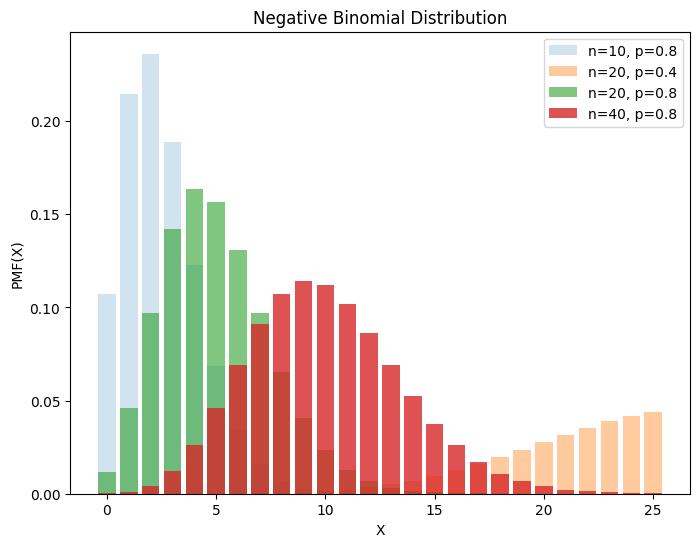
当\(r\)为整数时,又称 Pascal 分布。
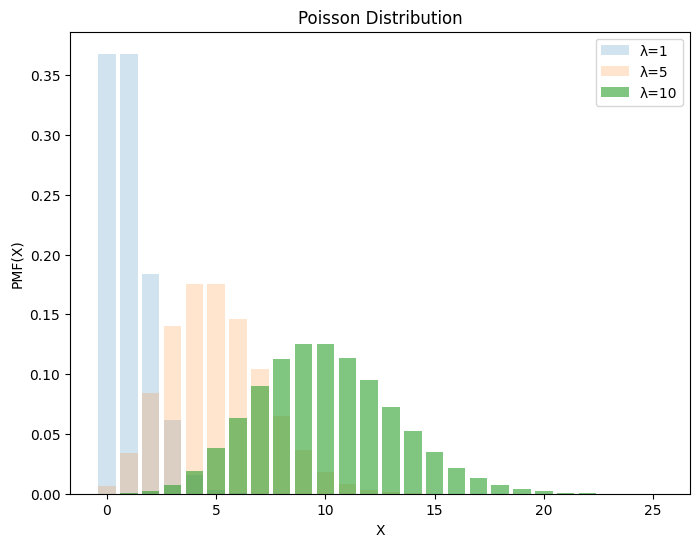
3.5. Poisson 分布#
Poisson 分布用于描述单位时间内随机事件发生的次数。将时间切分为\(n\)个时段,设某事件的总发生次数为\(λ\),则一个时段内该事件发生的概率为\(p= λ/n\),代入二项分布,
当\(n → ∞\)
得
Poisson 分布的均值、方差具有线性可加性。
λs = [1, 5, 10]
alphas = [0.2, 0.2, 0.6]
X = np.arange(0, 26, 1)
_, ax = plt.subplots(figsize=(8, 6))
for λ, alpha in zip(λs, alphas):
y = stats.poisson(mu=λ).pmf(X)
ax.bar(X, y, label=f"λ={λ}", alpha=alpha)
ax.set(xlabel="X", ylabel="PMF(X)", title="Poisson Distribution")
ax.legend()
plt.show()
3.6. 小结#
离散分布 |
表示 |
结果取值 |
常见情况 |
|---|---|---|---|
Bernoulli 分布 |
\(Bern(p)\) |
\(\{0, 1\}\) |
单样本互斥事件 |
二项分布 |
\(B(n, p)\) |
ℤ |
多样本互斥事件 |
超几何分布 |
\(H(N, m, n)\) |
ℤ |
不放回二项分布 |
Poisson 分布 |
\(Pois(λ)\) |
ℤ |
小概率事件 |
当\(n ≥ 20, p ⩽ 0.05\),\(B(n, p) → Pois(λ)\)
当\(np ≥ 5\),\(B(n, p) → 𝒩(np, np(1 - p))\)
当\(λ ≥ 20\),\(Pois(λ) → 𝒩(λ, λ)\)
当\(N → ∞\),\(H(N, m, n) → B(n, p)\)(当\(n\)固定,则\(p=M/N\)固定)
4. 常见连续分布#
4.1. 指数分布#
指数分布表示 Poisson 过程中的事件的时间间隔。可以看作是逆 Poisson 分布。
逆分布(inverse distribution)是随机变量的倒数服从的分布。
概率密度函数
其中,\(λ > 0\),是分布的参数,即每单位时间发生该事件的次数。
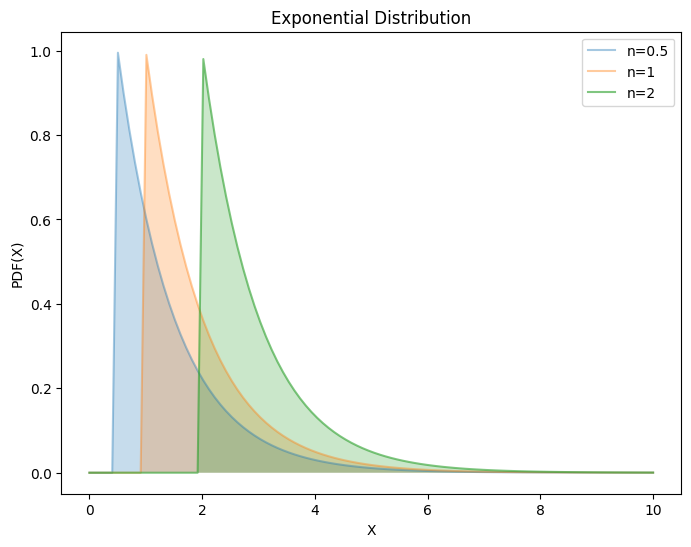
无记忆性
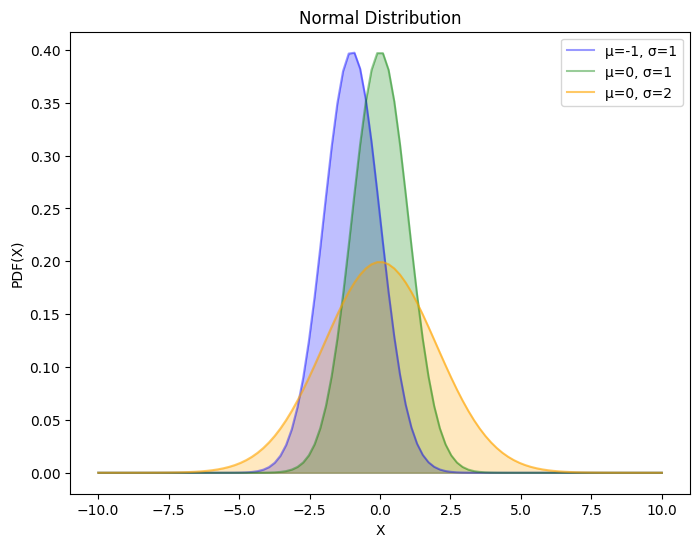
4.2. Gaussian 分布#
Gaussian 分布或 Gaussian 分布是所有分布函数中最重要的。这是由于所有分布函数的均值在足够大的样本数下都近似于 Gaussian 分布。
概率密度函数
该式由 de Moivre-LaPlace 中心极限定理首先给出,详见第二章。
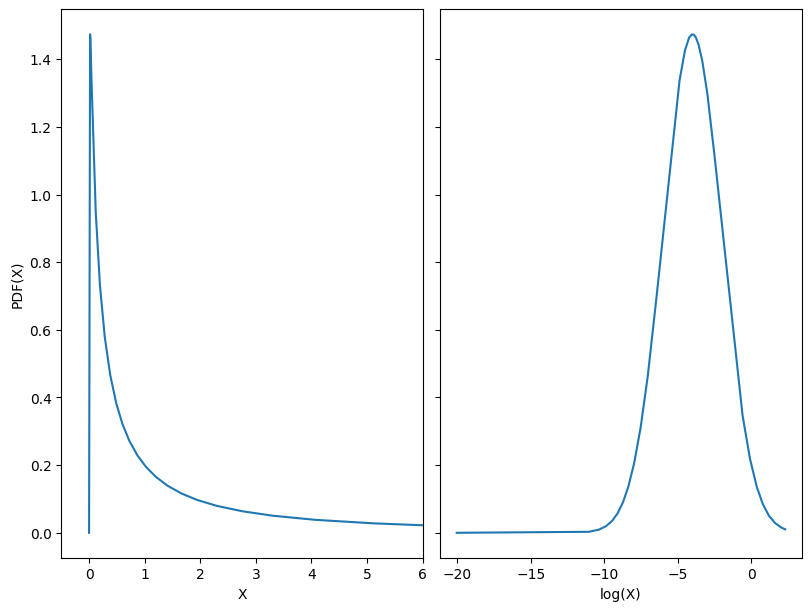
4.3. 对数 Gaussian 分布#
数据的对数正态变换通常用于将高偏度分布变换为 Gaussian 分布。
其中,\(s\)为形状参数。
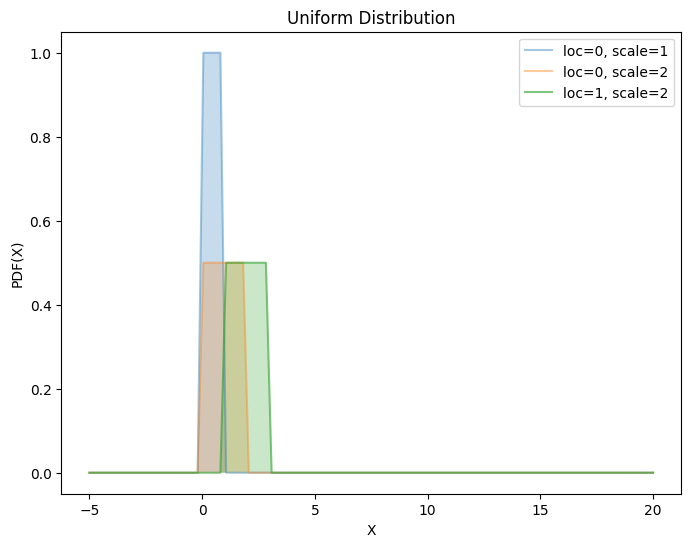
4.4. 均匀分布#
概率密度函数