统计量与抽样#
1. 统计量#
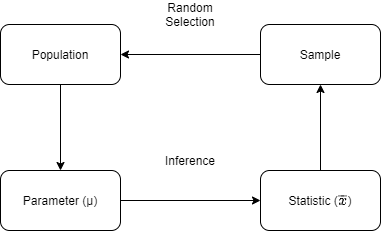
在数据的统计分析中,往往需要利用几个选定的样本(sample),得出其所来自的总体(population)的结论。正确的研究设计应该确保样本数据能够代表总体。
总体与样本之间的主要区别在于如何将观测结果分配到数据集中。
1.1. 集中程度#
术语 |
英文 |
定义 |
适用 |
|---|---|---|---|
算数均值 |
arithmetic mean |
\(\dfrac{∑X_{i}}{n}\) |
对称或近似对称资料 |
几何均值 |
geometric mean |
\(\sqrt{n}{∏X_{i}}\) |
百分数和比例表示的资料 |
调和均值 |
harmonic mean |
\(\dfrac{1}{\dfrac{1}{n} ∑\dfrac{1}{X_{i}}}\) |
速度类或有极端值的资料 |
中数 |
median |
\(M_d\) |
偏峰分布资料 |
众数 |
mode |
\(M₀\) |
1.2. 离散程度#
1.2.1. 极差、分位数#
极差(range):最大值 - 最小值;
分位数(percentile):多由箱线图表示,简单概括为\(5\)线\(n\)点,由上到下依次为:
上边缘:除离群值外的最大值
上四分位数:Q1,逆序排列,第 25% 个数
中位数:Q2
下四分位数:Q3,逆序排列,第 75% 个数
下边缘:除离群值外的最小值
若分位数计算结果不是整数,则取下一个整数
四分位距(inter-quartile-range,IQR):Q3 - Q1。< Q1 - 1.5 IQR 或 > Q1 + IQR 为离群值点;
IQR 无法将所有数据考虑进来,一般使用 \(μ ± 2*σ\)
1.2.2. 标准差、变异系数#
方差(variance):也叫平均平方偏差(mean square deviation)
标准偏差(standard deviation)
Python 中,NumPy 默认计算总体标准差,即分母为\(n\),而 Pandas 默认计算样本标准差
变异系数(coefficient of variation):用于量纲不同但变量间比较。
1.3. 期望#
期望值是该变量总体输出值的均值
对离散型分布
对连续型分布
设\(a\)为常数,\(X\)和\(Y\)是两个随机变量,则有
线性:\(𝔼[X + Y] = 𝔼[X] + 𝔼[Y]\)
\(𝔼[aX + Y) = a𝔼[X + Y]\)
独立性:\(X\)、\(Y\) 相互独立 ⇒ \(𝔼[XY) = 𝔼[X]𝔼[Y]\)
1.4. 方差#
设\(X\)为随机变量,若存在
则称其为\(X\)的方差,记作\(D(X)\)
即离均差的平方的期望
对离散型分布
对连续型分布
设\(a\)为常数,\(X\)和\(Y\)是两个随机变量
\(D(X) = 𝔼[X^2] - E^2(X)\)
\(D(aX + b) = a^2D(X)\)
独立线性可加:\(X\)、\(Y\)相互独立 ⇒ \(D(X + Y) = D(X) + D(Y)\)
\(D(X ± Y) = D(X) + D(Y) ± 2Cov(X, Y)\)
1.5. 协方差#
设\(X\)、\(Y\)为随机变量,若存在
则称其为\(X\)与\(Y\)的协方差,记作\(Cov(X, Y)\)
\(Cov(X, X) = D(X)\)
参数可交换:\(Cov(X, Y) = Cov(Y, X)\)
参数线性可加:\(Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y)\)
协方差构成的矩阵为对称阵
其中,\(σ^2\)是方差,亦为残差的均方误差(MSE)。
2. 大数定律#
2.1. Chebyshev 不等式#
设随机变量 \(X\) 的 \(𝔼[X] = μ, D(X) = σ^2\),则\(∀ϵ ∈ ℤ\),存在
即
推论
所有数据,至少 3/4 落在位于均值 2 个标准差范围内
所有数据,至少 8/9 落在位于均值 3 个标准差范围内
所有数据,至少 15/16 落在位于均值 4 个标准差范围内
2.2. 几乎确信收敛#
当\(n → ∞\),在函数\(P\)下,\(X_n(ω)\)不收敛到\(x₀(ω)\)的概率为 0
则称\(X_n\)几乎确信收敛\(x_0\),记为
2.3. Kolmogorov 大数定律#
也称强大数定律(Strong Law of Large Numbers,SLLN)。
设\(X_{i} ∼ i.i.d.\),且期望值\(𝔼[X_{i}] = μ(k = 1, 2, ⋯)\),则
2.3. 依概率收敛#
设\(X_2, X_2, ⋯\)是随机变量序列,若\(∀ϵ\),有
则称\(X_n\)依概率收敛于\(x_0\),记为
2.5. Wiener-Khinchin 大数定律#
也称弱大数定律(Weak Law of Large Numbers,WLLN)。定律指出:用算术均值来近似实际真值是合理的。
设\(X_{i} ∼ i.i.d.\),期望值\(𝔼[X_{i}] = μ(i = 1, 2, ⋯)\),则\(∀ϵ ∈ ℤ\),存在
当\(X_{i}\)为服从 0-1 分布,W-K 大数定律即为 Bernoulli 大数定律
3. 中心极限定理(CLT)#
3.1. 依分布收敛#
当\(X_n\)依分布收敛到\(x_0\),即\(X_n\)的 CDF 越来越接近\(x_0\)的 CDF(随机变量的 PDF 并不总存在)。\(\{X_n\}\)和\(\{x_0\}\)是 CDF 分别为\(\{F_n(⋅)\}\)和\(\{F_0(⋅)\}\)的随机变量序列,若在\(F_0(x)\)连续处,\(∀x ∈ ℝ\),有
则当\(n → ∞\)时,\(\{X_n\}\)依分布收敛于\(\{x_0\}\),记为
3.2. 独立同分布定理#
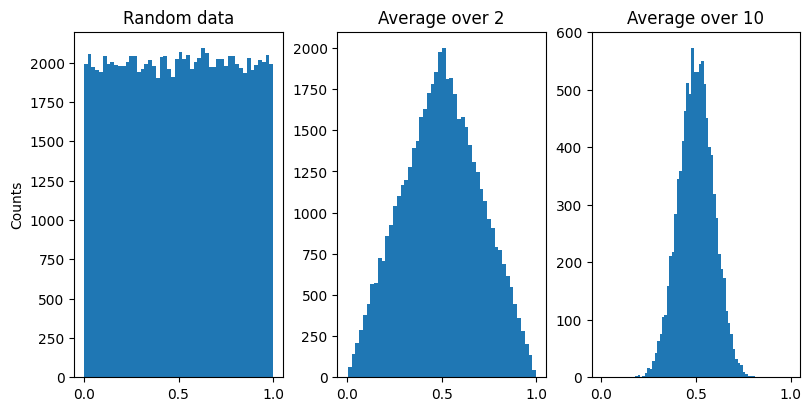
\(n\)个独立同分布随机变量之和近似于高斯分布。
当抽样次数足够大(\(n ≥ 30\))便有以上性质,这样的总体可看做正态总体。
3.3. De Moivre-LaPlace 定理#
设随机变量\(X_1, X_2, ⋯, X_n\ i.i.d. ∼ B(n, p)\),则\(∀ϵ ∈ ℤ\),存在
三种收敛对应大数定律和中央极限定理的三种收敛方式,前者关心的是一阶矩均值,后者不仅关心一阶矩,还关心二阶矩方差,也就是分布。从这个角度来看,矩在某种程度上统一了两者。当 \(n\)越来越大时,正态分布就变得越来越尖,趋于 ∞ 时,收敛为没有宽度的但无限高的的样子,有意思的是,其曲线下的面积却等于 1,被称为 Dirac-δ 函数,点电荷和点质量等点源和脉冲具有类似的性质。
4. 抽样分布#
4.1. 标准正态分布#
对正态分布,当\(μ = 0, σ = 1\)
称标准正态分布\(Φ(x)\),也叫 Z 分布。
\(Φ(x) = 1 - Φ(-x)\)
由此得到的统计量,称 Z 统计量。
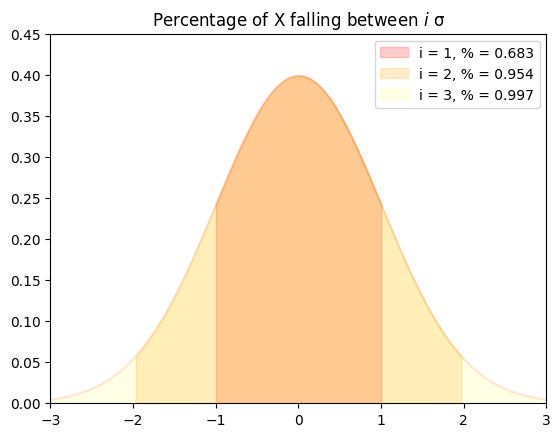
推论
68.27% 的数据落在距离均值 1 个标准差内
95.44% 的数据落在距离均值 2 个标准差内
99.74% 的数据落在距离均值 3 个标准差内
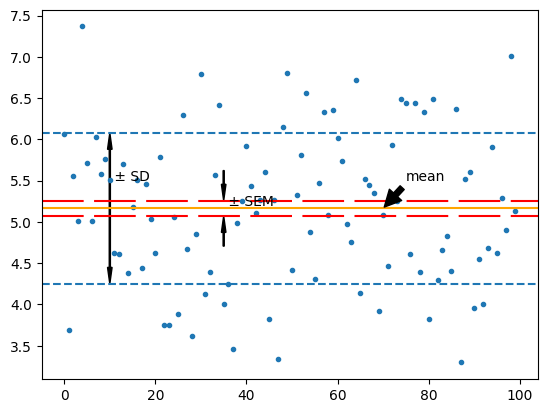
4.2. 抽样均值#
抽样均值
标准误差(standard error of the mean,SEM):系数标准偏差的估计值。
抽样方差
4.3. 独立分布之和#
由定义可得
4.3.1. \(χ^2\)分布#
\(χ^2\)分布用于描述高斯分布数据间的相关性(独立性)。
若\(∀X_{i} ∼ iid.\ 𝒩(0, σ^2)\)的随机变量,则
由\(Γ\)函数定义
当\(X_{i} ∼ 𝒩(0, 1)\),则
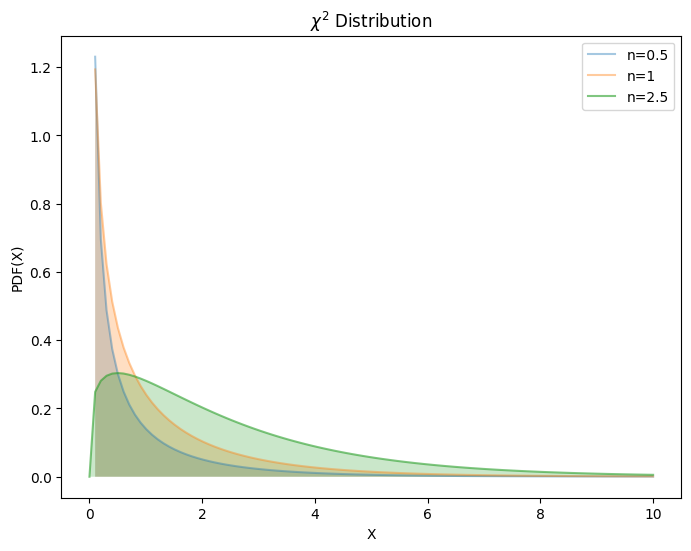
由\(Γ\)函数性质,其具有
取值非负性
线性可加性
均值为 \(n\),方差为 \(2n\)
4.4. 独立分布之商#
4.4.1. \(t\)分布#
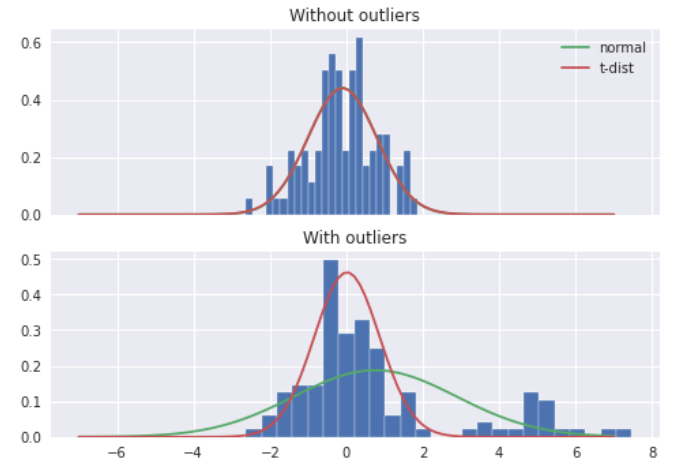
\(t\)分布,又称学生 \(t\)分布,是来自正态总体的样本均值的分布。通常用于小样本数,当总体均值及标准差未知时。\(t\)分布的实质是,用样本方差\(S\)估计总体方差\(σ\),也就是用标准误差(sem)代替 Z 统计量中的标准差。
由 CLT 可知,样本均值 \(x̄ ∼ 𝒩(μ, \dfrac{σ^2}{n})\)。
由于\(t\)分布的尾部长于高斯分布,因此受极端情况的影响要小得多
当\(X_1 ∼ χ^2(n), X_2 ∼ 𝒩(0, 1)\),则
令\(Z= \sqrt{X_1/n}\),则
可得,概率密度函数
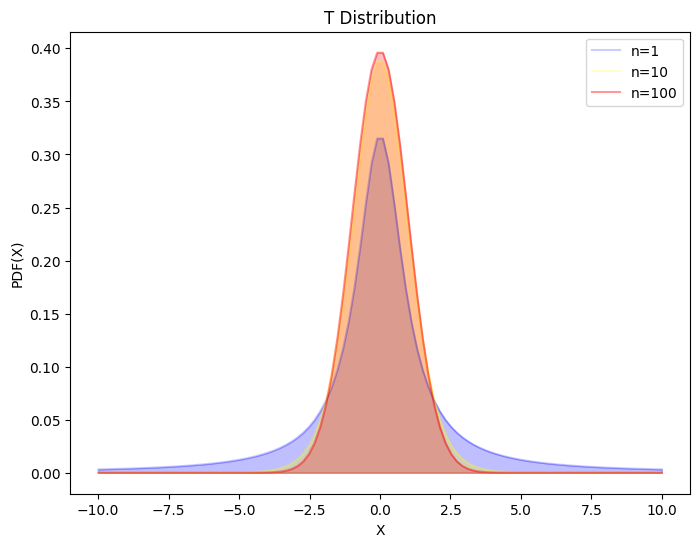
性质
对称性:t 分布关于 \(t = 0\) 对称
t 分布曲线的离散程度与自由度呈 \(n\) 负相关
\(n → ∞, \ t(n) → 𝒩(0, 1)\)
4.4.2. F 分布#
F 分布用于比较两组高斯分布数据的可变性,并确定方差分析的临界值,即判断两个总体是否有相同的方差。
当\(X_{i} ∼ χ^2(i)\),则
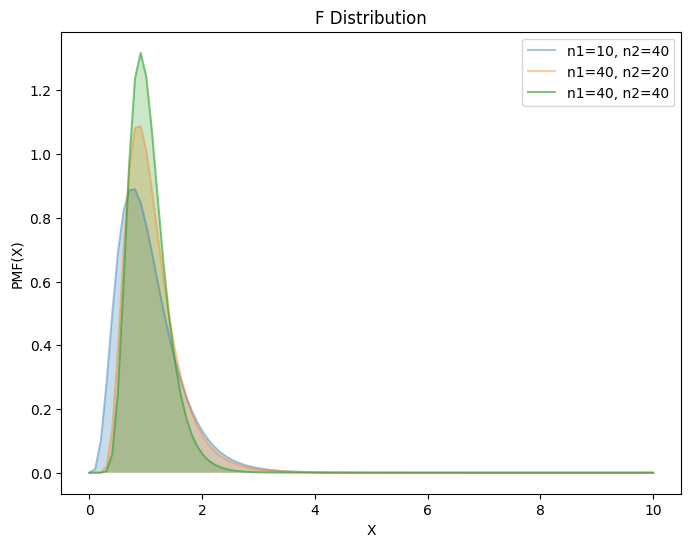
性质
如\(F ∼ F(m, n)\),则\(1/F ∼ F(n, m)\)
若\(t ∼ t(n)\),则\(t^2 ∼ F(1, n)\)
当\(X_{i} ∼ 𝒩(μ, σ^2)\),则
当\(X_{i} ∼ 𝒩(μ_1, σ_1^2), Y_{j} ∼ 𝒩(μ_2, σ_2^2)\),则
当\(σ_1^2 = σ_2^2\)
4.5. 小结#
抽样分布的前提设是总体相互独立
样本分布 |
总体分布 |
偏离量分布 |
统计量 |
|---|---|---|---|
\(χ^2\)分布 |
\(X_{i} ∼ 𝒩(0, 1)\) |
\(∑X_{i}^2\) |
|
\(t\)分布 |
\(X ∼ 𝒩(0, 1)\) |
\(Y ∼ χ^2(n)\) |
\(\dfrac{X}{\sqrt{Y/n}}\) |
\(F\)分布 |
\(X ∼ χ^2(m)\) |
\(Y ∼ χ^2(n)\) |
\(\dfrac{X/m}{Y/n}\) |

