细胞自动机#
1. 引言#
1.1. 构成#
细胞自动机(cellular automata,CA)是一个描述世界的模型,带有非常简单的物理。由冯·诺伊曼(John von Neumann,1903∼1957)和乌拉姆(Stanisław Marcin Ulam,1909∼1984)于 20 世纪 40 年代提出。
标准 CA 是一个由”细胞”、“细胞状态”、”邻域”和”状态更新规则”构成的四元组,数学上,可表示为
\(𝑨\):细胞自动机系统
\(L\):细胞空间
\(d\):细胞空间的维度
\(S\):细胞有限的、离散的状态集合
\(N\):某个邻域内所有细胞的集合
\(f\):局部映射或局部规则
1.2. 空间和邻居#
细胞:细胞自动机最基本的组成部分。细胞分布在离散的 Euclidean 空间位置上,每个时刻有着离散的状态,如 \(\{0, 1\}\) 等。
细胞空间:细胞所分布在 Euclidean 空间上的网格点的集合。最常见的为二维细胞空间,通常可按三角形、四边形和六边形三种网格排列。
邻居:细胞自动机的演化规则是局部的,对于指定细胞的状态进行更新时只需要知道其临近细胞的状态。某一细胞状态更新时要搜索的空间域称为该细胞的邻居。
邻居的划分:在四方网格划分下的二维细胞自动机的邻居通常有以下三种形式:
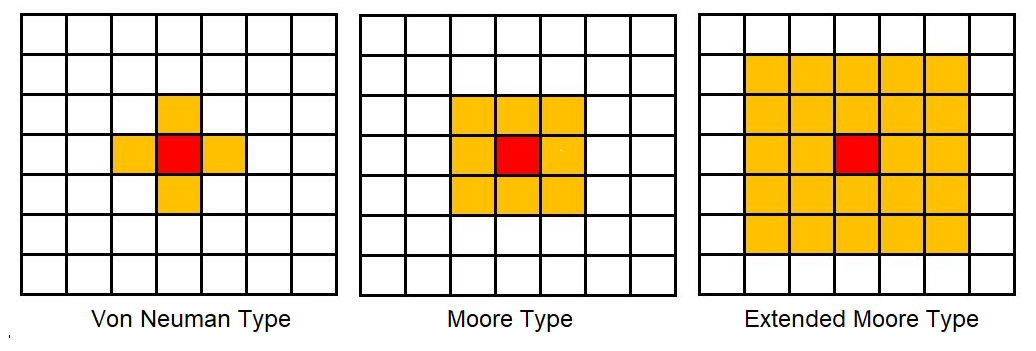
1.3. 边界#
边界条件:实际模拟细胞自动机的演化时不可能处理无限网络,系统必须是有边界的。处理边界格点时,可为边界的信息进行编码,由此选择不同的演化规则。另一种方法是在边界处扩展,以满足边界有与内部类似的邻居。
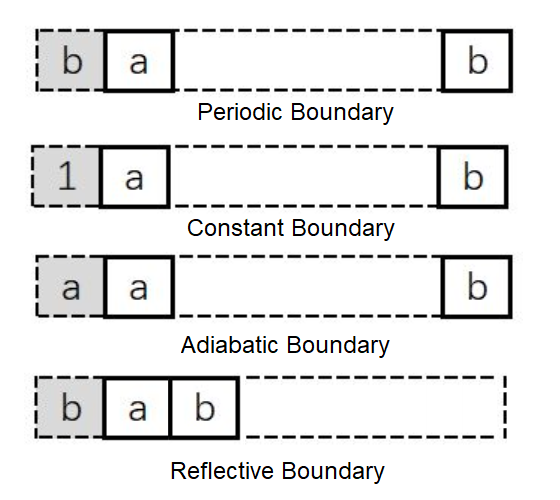
周期型边界:周期型是指相对边界连接起来的细胞空间。这种空间与无限空间最为接近,进行理论探讨时,常以此类空间作为实验进行模拟。
固定边界:所有边界外细胞均取某一固定常量。
绝热边界:边界外细胞的状态始终和边界细胞的状态保持一致。
反射边界:在边界外邻居的细胞状态是以边界细胞为轴的镜面反射
2. 简单 CA#
2.1. 零维 CA#
考虑带有单个细胞的 CA(也称零维 CA,不涉及空间)。细胞状态是用变 量\(x_i\)表示的整数,其中下标\(i\)表示\(x_i\)是时间步骤\(i\)期间的系统状态。作为初始条件,\(x_0 = 0\)。制定一个规则
执行简单的计算,即计数。
但,这个 CA 是不合规则的;可能的状态数通常是有限的。为了使其成立,选择状态个数\(k =2\),和另一个简单的规则
这个 CA 的行为很简单:闪烁。即,在每个时间步之后,细胞的状态在\(0\)和\(1\)之间切换。
大多数 CA 是确定性的,这意味着规则没有任何随机元素;给定相同的初始状态,它们总是产生相同的结果。也有不确定性的 CA,但这里不涉及它们。
2.2. 初等 CA#
初等 CA(elementary cellular automata)是状态集\(S\)只有两个元素,即状态个数\(k =2\),邻居半径\(r = 1\)的一维 CA。其邻居个数为\(N =2\)。这样的局部规则的映射函数可写为如下形式:
此时,输入状态一共有\(2^{2+1} = 8\)种组合方式。每个输入条件都对应着两种输出状态\(0\)或\(1\),一共存在\(2^8=256\)种状态组合。即,对于初等 CA 而言,总共存在\(256\)种规则。
假设一个细胞所具有的状态数为\(k\),所使用的的邻居半径为\(r\),则邻域内含\(2r+ 1\)个细胞,这样可能的输入条件的个数就是\(k^{2r+ 1}\),总的规则数为\(k^{k^{2r + 1}}\)。
2.3. 规则与分类#
沃尔夫勒姆(Stephen Wolfram,1959∼)在《一种新科学(A New Kind of Science)》和几篇从 80 年代中期开始的论文中根据 CA 呈现的范型(pattern)对 CA 进行了分类。按复杂性分类排序:
I 类(homogenous):自任何初始状态开始,经过一定时间运行后,细胞空间趋于一个空间平稳的构形,这里空间平稳即指每个细胞处于固定状态。不随时间变化而变化。
II 类(periodic):经过一定时间运行后,细胞空间趋于一系列简单的固定或周期范型。由于这些结构可看作是一种滤波器,故可应用到图像处理的研究中。
III 类(chaotic):自任何初始状态开始,经过一定时间运行后,细胞自动机表现出混沌的非周期行为,所生成的结构的统计特征不再变化,通常表现为分形分维特征。可用于产生随机数。
IV(complex):出现复杂的局部结构,或说是局部的混沌,其中有些会不断地传播。
2004 年,Wolfram 的研究助理 Matthew Cook 证明了初等 CA 中的规则 110 是通用的 [1],即,任何计算机可完成的任何计算都可由该 CA 完成。
2.4. 一维 CA#
在一维 CA 中,有三种自然范型:
有限序列:数量有限的细胞排成一排。除第一个和最后一个之外的所有细胞都有两个邻居。
环:数量有限的细胞排列成一个环。所有细胞都有两个邻居。
无限序列:数量无限的细胞排列成一排。
3. 二维 CA#
3.1. 生命游戏#
约翰·康威(John Horton Conway,1937∼2020)的生命游戏(GoL,1970)是一种使用 Moore 邻域的二维 CA,遵循简单的规则并产生令人惊讶的复杂行为。就像 Wolfram 的规则 110 一样,事实证明 GoL 是 Turing 完备的;即,至少在理论上它可计算任何可计算的函数。
在二维 CA 的所有可能规则中,大多数产生简单的行为:大多数初始条件快速稳定或无限增长。通过避免无趣的 CA,Conway 也避免了 Wolfram 的一类(固定)和二类(周期)行为,且可能还有三类(混沌)。
在 GoL 中,每个单元格的下一个状态取决于其当前状态和活动邻居的数量。这种规则可概括为 DSRO(Death, Survival, Reproduction, Overpopulation)。
若细胞的生前邻居数量 < D 或 > O,则细胞死亡;
若细胞的生前邻居数量 ⩽ S,则细胞存活;
若细胞的生前邻居数量 ≥ R 且 ⩽ O,则细胞复活。
当 DSRO = (2, 3, 3, 3),若一个细胞是活的,若它有两个或三个活动邻居就会生存,否则就会死亡。若一个细胞是死的,它将保持死亡,除非它恰好有三个邻居。
当前状态 |
邻居数量 |
下一个状态 |
|---|---|---|
生存 |
2∼3 |
生存 |
生存 |
0∼1, 4∼8 |
死亡 |
死亡 |
3 |
生存 |
死亡 |
0∼1, 4∼8 |
死亡 |
从最初的条件来看,GoL 会迅速达到稳定状态,活细胞数量几乎不变(可能带有一些振荡)。但,一些简单的开始条件,需要很长时间才能稳定下来,并产生令人惊讶的活细胞数量。这些模式被称为寿星(Methuselahs,《旧约·创世纪》中,一位活了 969 年的牧首)。
生命游戏非常接近于秩序与混沌的边界。若对 CA 的规则进行某种程度的改变,CA 可能会形成永恒的生长,以稳定的速度不断向外生长。另一种可能是,CA 变得非常混乱,以至于生命似乎是随机的,没有形成任何规律,没有保留一丝一毫的秩序,少量的秩序使 CA 具有生命力。生命游戏恰巧落在了两者之间,即属于此前提到的复杂型 CA。规则使其具有很好的不可预测性,有一些漂亮的模式和有趣的现象出现。
3.2. 生命的范型#
一般来说,稳定的生命范型至少有如下三类:
静物(still-life):静物形的状是稳定的,除非其他形状与之碰撞,可认为其周期为 1。常见形状有
块(block):由 4 个细胞组成,类似汉字的”田”;
蜂巢(beehive)
面包片(loaf)
舟(boat)
船(ship)
振荡器(oscillators):振荡器的形状会随着时间的推移而重复出现。例如,闪烁器(blinker)是一个周期为 2 的振荡器。它由 3 个连续线性细胞(上下或左右)组成,在水平方向和垂直方向之间旋转。
飞船(spaceship):可在生命世界中移动的形状被称为 “飞船”。例如,滑翔机(glider)由 5 个细胞组成,形成一个小箭头形状,周期为 4。
炮(gun)是一类特别的范型,它的主体部分会像振荡器一样,周期性地重复出现,也会周期性地发射出飞船。1970 年,自诩为黑客的 Bill Gosper 发现了第一把滑翔机炮(glider gun)。这一发现最终证明了康威的”生命游戏”是通用的,并能像图灵机一样工作。
3.3. Langton 蚂蚁#
Langton 蚂蚁是另一个经典的二维 CA,由克里斯·朗顿(Chris Langton,1948 ∼)于 1986 年提出 [2]。平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只”蚂蚁”。蚂蚁的头部朝向为:上下左右其中一方。蚂蚁的移动规则十分简单:
若蚂蚁在黑格,右转 \(90°\),将该格改为白格,并向前移一格;
若蚂蚁在白格,左转 \(90°\),将该格改为黑格,并向前移一格。
规则虽然简单,蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称,像是会重复,但不论起始状态如何,蚂蚁经过漫长的混乱活动后,会开辟出一条规则的”高速公路”。
3.4. \(λ\) 法则#
Langton 对 CA 的另一个重要贡献是提出了\(λ\)法则,通过该法则,可对任一个 CA 的可预测性进行分类。 起初,Langton 做了一个量表;量表的范围在 0 到 1 之间,0 表示固定的、有序的、可预测的。当按小数点往上爬时,刻度的”面积”就从有序变成了所谓的周期性,然后又变成了复杂,最后,在这之上,就是混沌。
要计算出 CA 的\(λ\)值很容易。它仅是一个细胞的新状态所处的规则的分数,用小数表示。即,导致生命的规则越多,\(λ\)值就越大。在 CA 中,棋盘上的细胞越多,平面就越混沌。当棋盘变得更自由时,它就会变得有序。因为 CA 要简化得多,通常每个单元格都有 2 个状态,故通常把死亡看成是”清场”。
这种\(λ\)值的效果出奇的好。以 Wolfram 的一维 CA 为例。若把细胞的状态算作邻居的话,有 3 个邻居,故有\(2^3 = 8\) 个不同的规则(相比之下,生命游戏是 512 个)。设置背景状态为 0,对于任意表,计算表中非零元素个数。\(λ\)的计算公式如下:
其中,\(s\)为每个细胞的状态个数,\(n\)为邻域集合大小,\(n_q\)为非零元素个数。
对于\(λ\)讨论结果大致如下:
\(λ ∈ [0, 0.1]\)时,所有细胞被吸引至某种固定状态,此时的 CA 属于固定型;
\(λ ≈ 0.2\)时,系统在一些固定状态下循环,此时 CA 属于周期型;
\(λ = 0.3\)时,CA 开始趋向于复杂型;
\(λ ∈ [0.3, 0.6]\)时,此时 CA 属于复杂型,复杂度随\(λ\)递增;
\(λ ∈ [0.6, 1.0]\)时,系统复杂结构消失,此时 CA 属于混沌型;
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|---|---|---|---|---|---|---|---|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
上表有 4 个规则代表生,\(λ = 1 -4/2^3 = 0.5\)。这似乎是个不错的值,使这个 CA 落入复杂领域。
